if sample size increases what happens to margin of error

How is Sample Size Related to Standard Error, Ability, Confidence Level, and Event Size?
Using graphs to demonstrate the correlations
When conducting statistical assay, especially during experimental design, 1 practical issue that one cannot avoid is to determine the sample size for the experiment. For case, when designing the layout of a web folio, nosotros want to know whether increasing the size of the click button volition increase the click-through probability. In this case, AB testing is an experimental method that is commonly used to solve this problem.
Moving to the details of this experiment, you volition get-go make up one's mind how many users I will need to assign to the experiment group, and how many we demand for the control grouping. The sample size is closely related to four variables, standard fault of the sample, statistical power, conviction level, and the effect size of this experiment.
In this commodity, we will demonstrate their relationships with the sample size by graphs. Specifically, we will talk over different scenarios with 1-tail hypothesis testing.
Standard Error and Sample Size
The standard error of a statistic corresponds with the standard deviation of a parameter. Since it is nearly impossible to know the population distribution in near cases, nosotros can approximate the standard divergence of a parameter by computing the standard error of a sampling distribution. The standard mistake measures the dispersion of the distribution. As the sample size gets larger, the dispersion gets smaller, and the mean of the distribution is closer to the population hateful (Central Limit Theory). Thus, the sample size is negatively correlated with the standard error of a sample. The graph below shows how distributions shape differently with different sample sizes:

As the sample size gets larger, the sampling distribution has less dispersion and is more than centered in by the hateful of the distribution, whereas the flatter curve indicates a distribution with higher dispersion since the data points are scattered across all values.
Understanding the negative correlation between sample size and standard mistake help conduct the experiment. In the experiment blueprint, it is essential to constantly monitor the standard mistake to run into if we need to increase the sample size. For example, in our previous example, we want to run across whether increasing the size of the bottom increases the click-through rate. The target value we need to measure in both the control group and the experiment group is the click-through rate, and it is a proportion calculated equally:
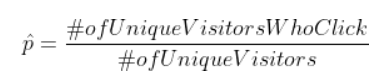
the standard error for a proportion statistic is:
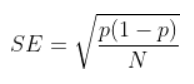
The standard error is at the highest when the proportion is at 0.5. When conducting the experiment, if observing p getting shut to 0.five(or 1-p getting close to 0.five), the standard error is increasing. To maintain the same standard error, nosotros need to increase N, which is the sample size, to reduce the standard error to its original level.
Statistical Power and Sample Size
Statistical ability is likewise called sensitivity. It is calculated past 1- β, where β is the Type Two error. College power means y'all are less likely to make a Type II error, which is failing to decline the nix hypothesis when the null hypothesis is faux. As stated here:
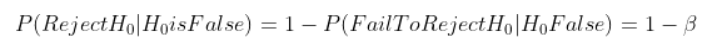
In other words, when reject region increases (credence range decreases), it is likely to reject. Thus, Type I error increases while Type 2 error decreases. The graph below plots the relationship among statistical power, Blazon I error (α) and Type II error (β) for a 1-tail hypothesis testing. After choosing a confidence level (ane-α), the blue shaded area is the size of power for this item assay.
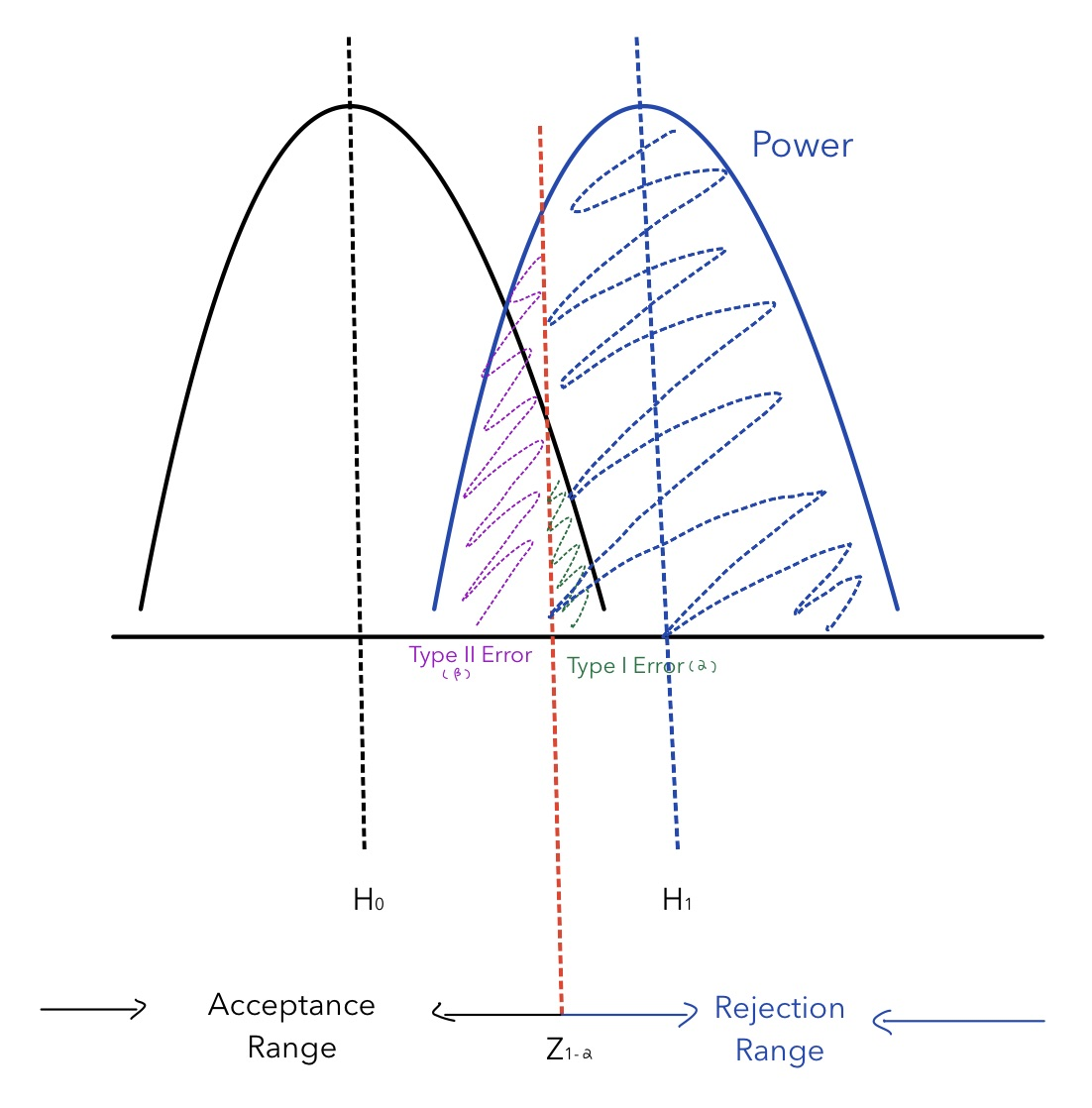
From the graph, it is obvious that statistical ability (1- β) is closely related to Type II error (β). When β decreases, statistical ability (ane- β) increases. Statistical power is also afflicted to Type I error (α), when α increases, β decreases, statistical power (1- β) increases.
The red line in the heart decides the tradeoff between the acceptance range and the rejection range, which determines the statistical power. How does the sample size affect the statistical power? To answer this question, we need to change the sample size and see how statistical power changes. Since Type I mistake as well changes corresponded with the sample size, we need to hold it constant to uncover the relationship between the sample size and the statistical ability. The graph below illustrates their human relationship:
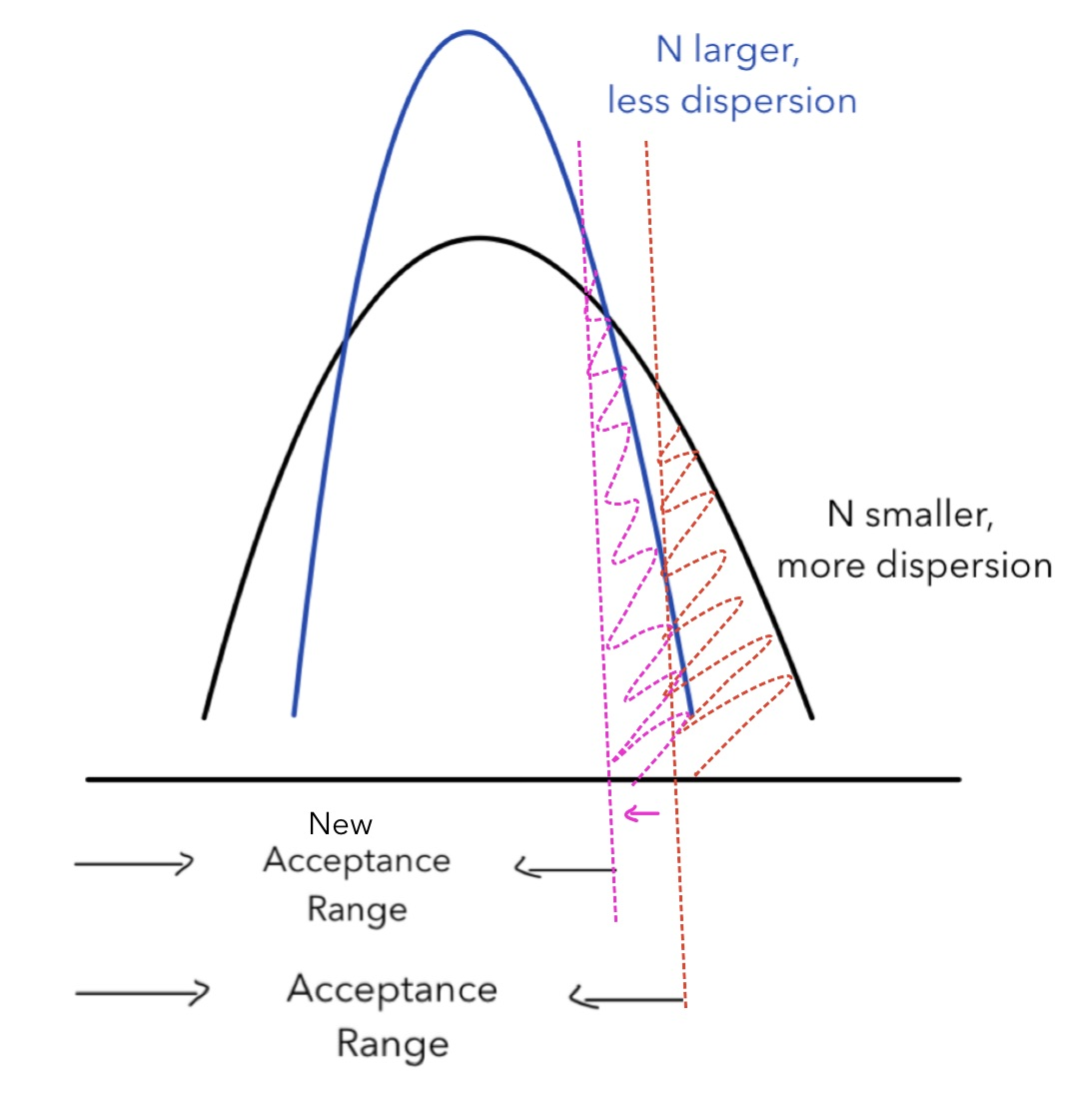
When the sample size increases, the distribution will be more concentrated effectually the mean. To agree Type I error abiding, we need to subtract the critical value (indicated by the cherry-red and pink vertical line). As a result, the new acceptance range is smaller. As stated above, when it is less likely to take, information technology is more than likely to pass up, and thus increases statistical power. The graph illustrates that statistical power and sample size have a positive correlation with each other. When the experiment requires higher statistical power, you need to increment the sample size.
Conviction Level and Sample Size
As stated above, the confidence level (one- α) is also closely related to the sample size, as shown in the graph beneath:
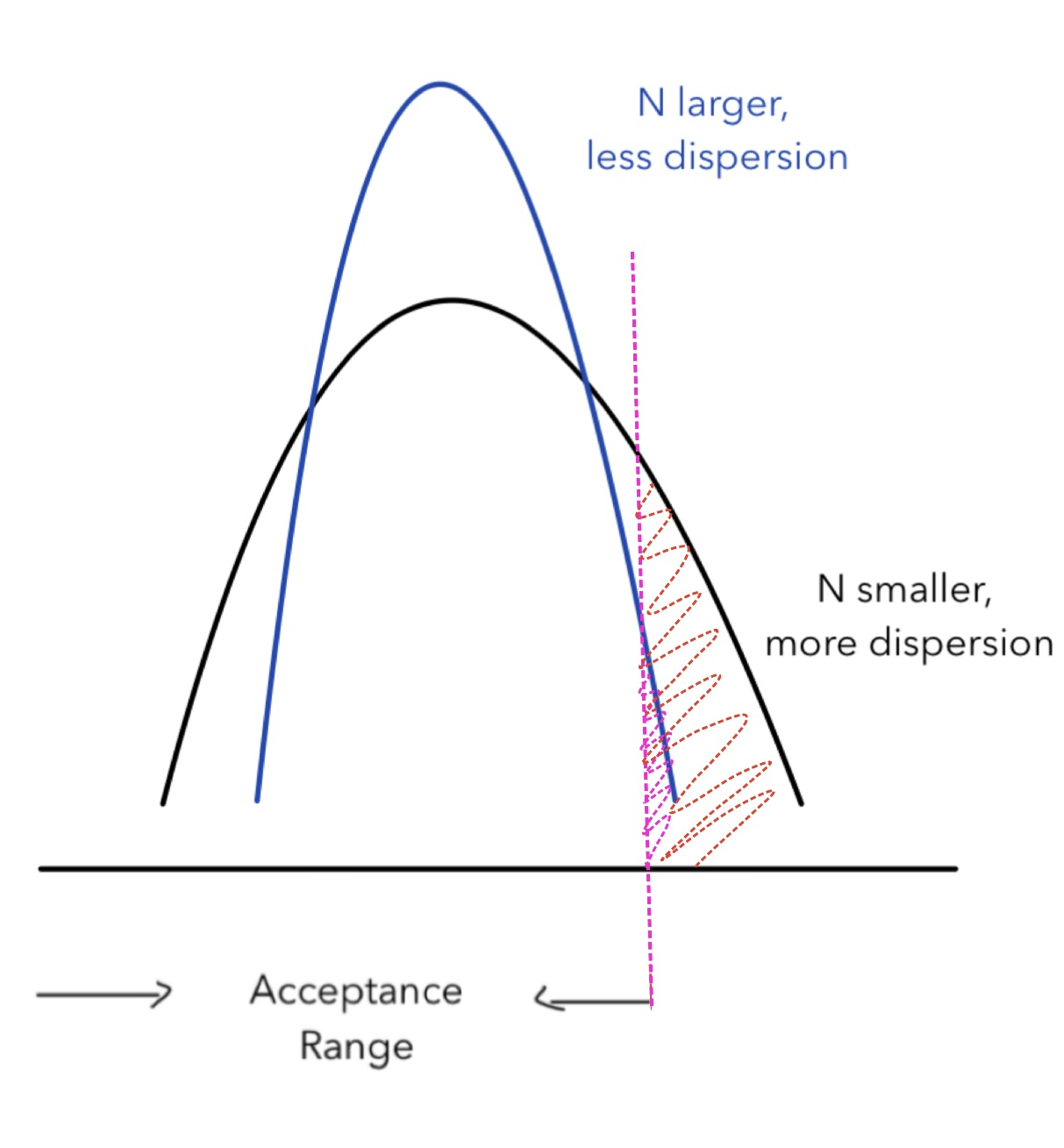
Equally the acceptance range keeps unchanged for both bluish and black distributions, the statistical power remains unchanged. Equally the sample size gets larger (from black to bluish), the Type I error (from the red shade to the pink shade) gets smaller. For one-tail hypothesis testing, when Type I mistake decreases, the confidence level (1-α) increases. Thus, the sample size and confidence level are also positively correlated with each other.
Upshot Size and Sample Size
The effect size is the practical meaning level of an experiment. It is set by the experiment designer based on practical situations. For example, when we want to bank check whether increasing the size of the bottom in the webpage increases the click-through probabilities, we need to define how much of a difference we are measuring betwixt the experiment grouping and the command group is practically significant. Is a 0.1 departure significant enough to concenter new customers or generate significant economic profits? This is the question the experiment designer has to consider. Once the upshot size is set, nosotros can use it to decide the sample size, and their relationship is demonstrated in the graph below:
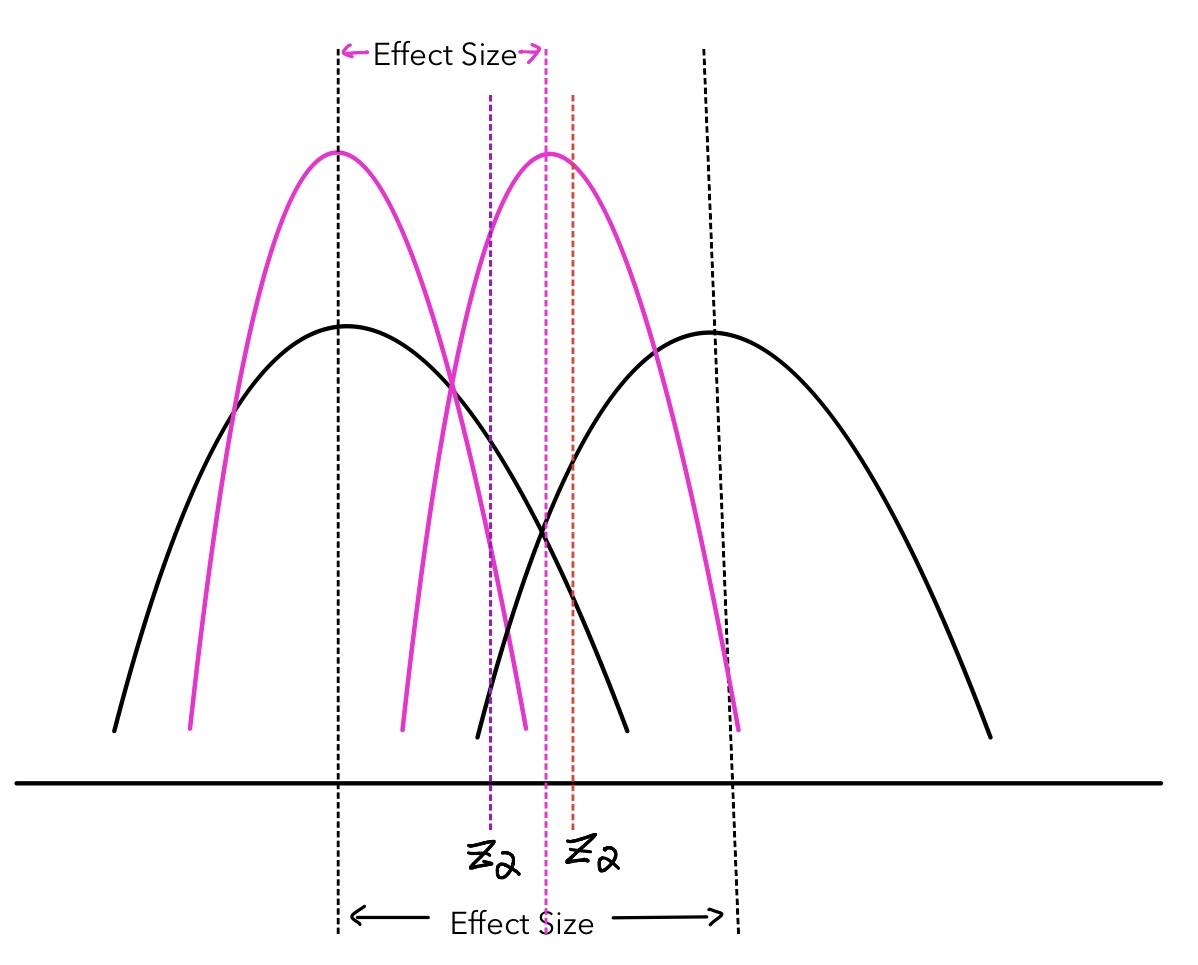
As the sample size increases, the distribution go more than pointy (blackness curves to pink curves. To proceed the conviction level the same, we need to move the disquisitional value to the left (from the carmine vertical line to the royal vertical line). If we do not motion the alternative hypothesis distribution, the statistical ability volition decrease. To maintain the constant power, nosotros demand to move the alternative hypothesis distribution to the left, thus the constructive effect decreases every bit sample size increases. Their correlation is negative.
How to interpret the correlations discussed above?
In summary, we have the following correlations between the sample size and other variables:

To interpret, or better memorizing the human relationship, we can see that when we need to reduce errors, for both Type I and Type II error, we need to increase the sample size. A larger sample size makes the sample a better representative for the population, and it is a better sample to use for statistical assay. Equally the sample size gets larger, it is easier to detect the deviation between the experiment and control grouping, even though the difference is smaller.
How to calculate the sample size given other variables?
There are many ways to summate the sample size, and a lot of programming languages have the packages to calculate it for you lot. For example, the pwr() parcel in R can do the piece of work. Compared to knowing the exact formula, it is more of import to understand the relationships behind the formula. Promise this article helps y'all sympathize the relationships. Cheers for reading!
Here is the list of all my blog posts. Bank check them out if you lot are interested!
Source: https://towardsdatascience.com/how-is-sample-size-related-to-standard-error-power-confidence-level-and-effect-size-c8ee8d904d9c
0 Response to "if sample size increases what happens to margin of error"
Post a Comment